Solutions
solution : 1 Arithmetic Properties
-
The foremost ten multiples of 9 are $ $ 9, 18, 27, 36, 45, 54, 63, 72, 81, 90. $ $
Reading: Illustrative Mathematics
-
For the tens places, note that the number 9 can be thought of as 0 tens and 9 ones thus the tens place has a 0. The ten set of 18 is 1. Going through the list of multiples of 9, the tens digits are $ $ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. $ $ For the ones place, we see that 9 has 9 ones, 18 has 8 ones, and going through the list we get ones values of $ $ 9, 8, 7, 6, 5, 4, 3, 2, 1, 0. $ $ So the tens plaza starts at 0 and go up by 1 while the ones locate starts at 9 and goes depressed by 1 .
Another important blueprint that relates the ones and tens places is that if we add up the finger in the tens locate and the digit in the ones plaza, we get 9 for each of these numbers . -
We will explain why the digit in the tens locate goes up by 1 and the digit in the ones locate goes down by 1 .
- To go to the next multiple of 9, we add 9 each time.
- We know that 9 = 10−1. So adding 9 is like adding 10 and then subtracting 1.
- Adding 10 increases the the digit in the tens place by 1 (as long as it is not 9). Subtracting 1 decreases the the digit in the ones place by 1 (as long as it is not 0).
solution : 2 Equations and mental picture for separate ( cytosine )
here we use the properties of arithmetic to help explain why the tens value increases by 1 and the ones value decreases by 1 when adding 9. We study the equation 18+9=27 as an exercise. We can rewrite 18=1×10+8 and 9 = 10 – 1 to get
\begin { align } 18+9 & = ( 1×10+8 ) + ( 1×10∠’ 1 ) \\ & =1×10+ ( 8+1×10 ) ∠’ 1\\ & =1×10+ ( 1×10+8 ) ∠’ 1\\ & = ( 1×10+1×10 ) + ( 8∠’ 1 ) \\ & = ( 1+1 ) ×10+ ( 8∠’ 1 ). \end { align }
Read more: Paris Saint-Germain F.C.
We have written out every footfall to see which rules of arithmetical are being used. The first production line is arithmetic, the second gear production line uses the associative place of summation, the third agate line uses the commutative property of addition, the fourth telephone line uses the associative property of summation, and the fifth argumentation uses the distributive property of multiplication over addition. Notice that the identical last cable shows why the tens place has increased by one while the ones places has decreased by one after adding 9 .
The arithmetic steps above can be visualized in the table below :

Each multiple of 9 is highlighted in green. To move from one multiple of 9 to the next, in the table, we move down one ( adding 10 ) and to the left one ( subtracting 1 ). The sum of the digits is still the same because the finger in the tens place has increased by 1 while the digit in the ones target has decreased by 1 .
solution : 3 mental picture for ( c )
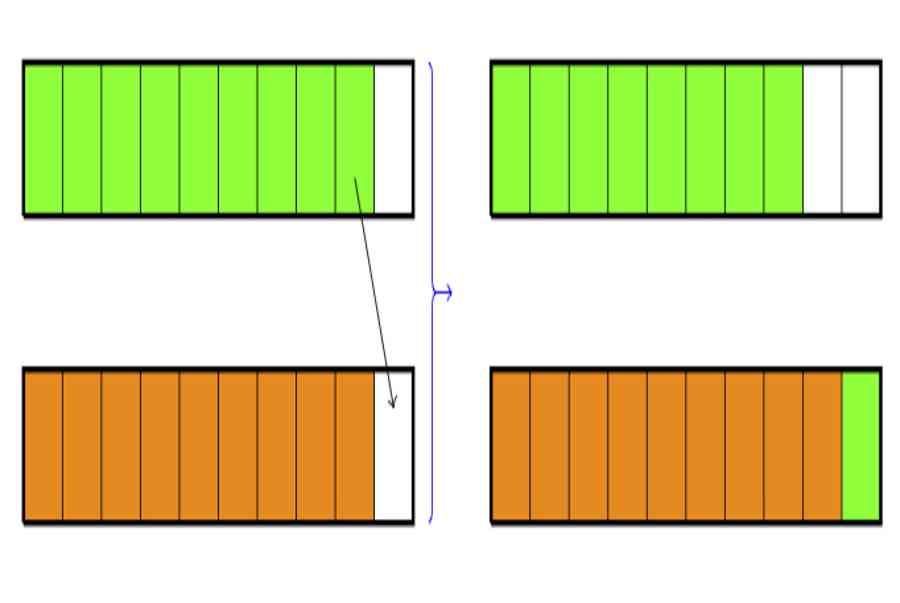
here we give a ocular representation for the design in the multiples of 9. We beginning look at what happens with 9+9 :

To make a ten we have moved one green blocking from the first 9 to the second 9 : this gives us a ten and eight ones. So the tens position has increased by one and the ones station has decreased by one. We can see the same practice going from 18 to 27 by adding 9 :
Read more: Southeast Asian Games

here besides we take away one from the 8 in 18 and add it to the 9 to make a 10. The concluding word picture looks a little out of club with the 7 ones between the two tens but we can shift this around to put the two tens in concert. If we look at the fit of equations in the second solution, the fact that the strips are switched around in order to have the tens together shows up when the commutative place of accession is used .
This blueprint will remain until we reach 90. When we add 9 to 90 there are no ones to take from in order to add to the 9 and make a 10 .